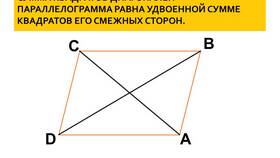
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны. Для данной геометрической фигуры существует важная теорема о сумме квадратов его сторон.
Содержание
Теорема о сумме квадратов сторон
Сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей. Математически это выражается формулой:
- 2a² + 2b² = d₁² + d₂²
Где:
- a и b - длины смежных сторон параллелограмма
- d₁ и d₂ - длины диагоналей
Доказательство теоремы
Теорема доказывается с помощью теоремы косинусов:
- Рассмотрим треугольник, образованный двумя сторонами и первой диагональю
- Запишем теорему косинусов для этого треугольника
- Рассмотрим треугольник, образованный теми же сторонами и второй диагональю
- Сложим полученные уравнения
Пример расчета
| Параметры | Значения |
| Сторона AB = CD | 5 см |
| Сторона AD = BC | 7 см |
| Диагональ AC | 8 см |
| Диагональ BD | 6 см |
| Сумма квадратов сторон | 2×5² + 2×7² = 148 |
| Сумма квадратов диагоналей | 8² + 6² = 100 (не соответствует, значит такие параметры невозможны) |
Практическое применение
- Проверка корректности параметров параллелограмма
- Вычисление неизвестных параметров фигуры
- Решение геометрических задач на построение
- Применение в технических расчетах
Данное свойство параллелограмма является важным инструментом в геометрических расчетах и находит применение в различных областях математики и ее приложений.